volver al índice

Tema 3: Cálculo Integral de Varias Variables

• 1. Integrales Dobles
• 2. Integrales Triples
• 3. Cambio de Variables
• Ejercicios

1. Integrales Dobles

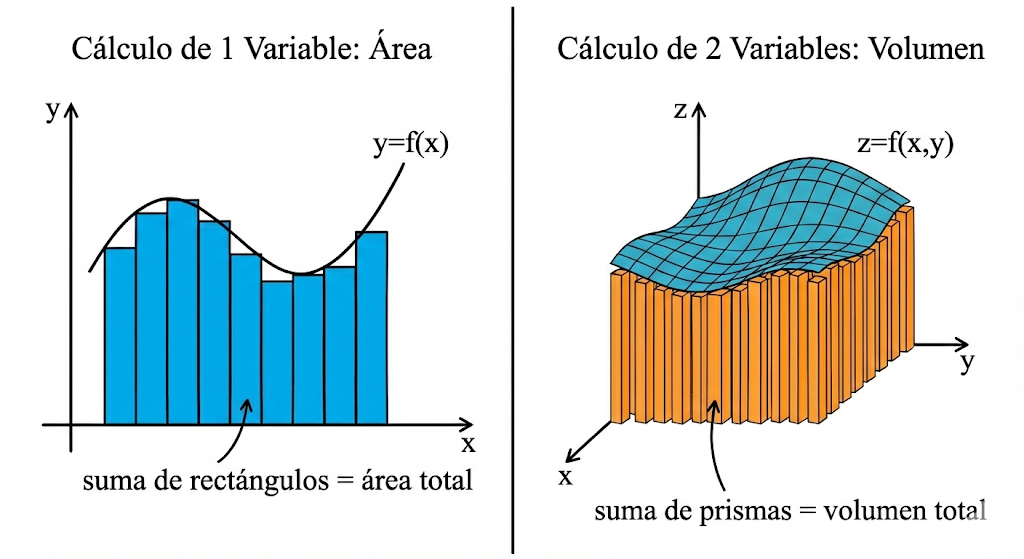
Idea: De manera análoga a cómo en una variable sumamos una infinidad de rectángulos diminutos para calcular el área bajo una curva, en el cálculo de varias variables extendemos este concepto. Con las integrales dobles, sumamos una infinidad de prismas rectangulares infinitesimalmente delgados para determinar el volumen total que se encuentra bajo una superficie.

Teorema de Fubini

Permite calcular integrales dobles como integrales iteradas (o sucesivas).

• Sobre Rectángulos: Si $\mathrm{\Omega }=[a,b]\times [c,d]$:

• Sobre Regiones Generales:
  • Tipo I (Vertical): $\mathrm{\Omega }=\{(x,y)\in {\mathbb{R}}^2:a\le x\le b,g_1(x)\le y\le g_2(x)\}$,

- Tipo II (Horizontal): $\mathrm{\Omega }=\{(x,y)\in {\mathbb{R}}^2:c\le y\le d,h_1(y)\le x\le h_2(y)\}$,

Cambio de Orden de Integración

Consiste en describir una región de Tipo I como una región de Tipo II (o viceversa) para facilitar la integración. Es fundamental dibujar la región de integración.

Aplicaciones

• Volumen bajo superficie: $V={\iint }_{\mathrm{\Omega }}(z_{techo}(x,y)-z_{suelo}(x,y))dA$
• Área (2D): $A(\mathrm{\Omega })={\iint }_{\mathrm{\Omega }}1dA$

Dada una lámina $\mathrm{\Omega }$ con función de densidad superficial $\sigma (x,y)$:

• Masa: $M={\iint }_{\mathrm{\Omega }}\sigma (x,y)dA$
• Centro de Gravedad $(\overline{x},\overline{y})$:
  • $\overline{x}=\frac{M_y}{M}$
  • $\overline{y}=\frac{M_x}{M}$
    siendo
  • $M_x={\iint }_{\mathrm{\Omega }}y\cdot \sigma (x,y)dA$
  • $M_y={\iint }_{\mathrm{\Omega }}x\cdot \sigma (x,y)dA$
    Nota: Si la densidad es constante, el centro de gravedad se llama centroide.

2. Integrales Triples

Se calculan de forma análoga a las dobles, usando el Teorema de Fubini.

• Sobre Cajas Rectangulares: Si $\mathrm{\Omega }=[a,b]\times [c,d]\times [e,f]$:

  $${\iiint }_{\mathrm{\Omega }}f(x,y,z)dV={\int }_a^b{\int }_c^d{\int }_e^{f}f(x,y,z)dzdydx\text{(y los otros 5 órdenes)}$$

Ejemplo:
Calcular la integral de la función $f(x,y,z)=x+yz$ sobre la caja $B=[0,1]\times [0,2]\times [0,1]$.
Al ser una caja rectangular, los límites son constantes. Podemos elegir cualquier orden. Usaremos el orden $dzdydx$.

Resolución paso a paso:
$$\int_0^1 (x + yz) , dz = \left[ xz + y\frac{z^2}{2} \right]{z=0}^{z=1} = \left(x(1) + \frac{y}{2}\right) - 0 = x + \frac{y}{2}$$
$$\int_0^2 \left( x + \frac{y}{2} \right) , dy = \left[ xy + \frac{y^2}{4} \right]^{y=2} = \left(2x + \frac{4}{4}\right) - 0 = 2x + 1$$
$$\int_0^1 (2x + 1) , dx = \left[ x^2 + x \right]_0^1 = (1+1) - 0 = \mathbf{2}$$

• Sobre Regiones Generales: Si $W\subset {\mathbb{R}}^3$ se proyecta sobre una región $\mathrm{\Omega }$ en el plano $XY$, y está limitada superior e inferiormente por $z=u_2(x,y)$ y $z=u_1(x,y)$:

  $${\iiint }_{W}f(x,y,z)dV={\iint }_{\mathrm{\Omega }}({\int }_{u_1(x,y)}^{u_2(x,y)}f(x,y,z)dz)dA$$
  • Otra forma de hacerlo consiste en proyectar sobre el eje $z$, dando lugar a un intervalo $[a,b]$, y luego integrar la sección horizontal (rebanadas) ${\mathrm{\Omega }}_z$ resultante para cada $z$:
  $${\iiint }_{W}f(x,y,z)dV={\int }_a^b({\iint }_{\mathrm{\Omega }(z)}f(x,y,z)dA)dz$$

  Ejemplo: Imagina un tetraedro (una pirámide triangular) limitado por los planos coordenados ($x=0,y=0,z=0$) y el plano inclinado $x+y+z=1$.

El objetivo: Calcular ${\iiint }_{W}2zdV$ usando el método de rebanadas horizontales.

• Límites de $z$: El sólido va desde el suelo ($z=0$) hasta el pico más alto donde $x=0,y=0$, por lo que $z=1$. El intervalo es $[0,1]$.

• La sección $\mathrm{\Omega }(z)$: Para un $z$ fijo, cortamos la pirámide horizontalmente. La forma resultante es un triángulo en el plano $XY$ limitado por $x=0$, $y=0$ y la recta $x+y=1-z$ (despejando de la ecuación del plano).

Planteamiento:

La integral se ve así: ${\int }_0^1[{\iint }_{\mathrm{\Omega }(z)}f(x,y,z)dA]dz$

1. Resolvemos primero la integral doble (la rebanada):

   Como la función a integrar es $2z$, y dentro de la integral doble $z$ es una constante, podemos sacarla fuera de la integral interior:

   $${\iint }_{\mathrm{\Omega }(z)}2zdA=2z\cdot {\iint }_{\mathrm{\Omega }(z)}1dA=2z\cdot \text{Área}(\mathrm{\Omega }(z))$$

   Nota: $\iint 1dA$ es simplemente el área de la región.

   La región $\mathrm{\Omega }(z)$ es un triángulo rectángulo con catetos de longitud $(1-z)$.

   $$\text{Área}=\frac{\text{base}\cdot \text{altura}}{2}=\frac{(1-z)(1-z)}{2}=\frac{(1-z{)}^2}{2}$$

   Por tanto, el resultado de la integral interior es:

   $$2z\cdot \frac{(1-z{)}^2}{2}=z(1-z{)}^2$$

2. Resolvemos la integral exterior (respecto a $z$):

   Ahora integramos ese resultado desde $z=0$ hasta $z=1$:

   $$I={\int }_0^{1}z(1-z{)}^{2}dz$$

   Expandimos el binomio: $(1-z{)}^2=1-2z+z^2$. Multiplicamos por $z$:

   $$I={\int }_0^1(z-2z^2+z^3)dz$$

   Calculamos la primitiva:

   $${[\frac{z^2}{2}-\frac{2z^3}{3}+\frac{z^4}{4}]}_0^1=\frac{1}{2}-\frac{2}{3}+\frac{1}{4}$$

   Mínimo común múltiplo (12):

   $$\frac{6}{12}-\frac{8}{12}+\frac{3}{12}=\frac{1}{12}$$

Resultado Final: $\frac{\mathbf{1}}{\mathbf{12}}$

Aplicaciones en Sólidos (3D)

Dada una región sólida $W$ con función de densidad volumétrica $\rho (x,y,z)$:

• Masa: $M={\iiint }_W\rho (x,y,z)dV$

3. Cambio de Variables

Jacobiano

Si un cambio de variables viene dado por $x=x(u,v)$ e $y=y(u,v)$, el Jacobiano de la transformación es:

La fórmula del cambio de variable es:

Para 3D, el Jacobiano es el determinante de la matriz 3x3 de derivadas parciales.

Coordenadas Polares (en 2D)

Es un cambio de variable específico para simetría circular.

• Transformación: $x=r\cos \theta$, $y=r\sin \theta$
• Jacobiano: $J(r,\theta )=r$
• Elemento de área: $dA=rdrd\theta$

Ejemplo: volumen bajo un Paraboloide

Imagina que queremos calcular la integral doble de la función $f(x,y)=x^2+y^2$ sobre una región $D$, donde $D$ es un círculo centrado en el origen con radio 2.

Si intentáramos resolver esto con $x$ e $y$, la integral se vería así:

Resolver esas raíces cuadradas dentro de la integral es largo y complicado.
Transformaremos todo a términos de radio ($r$) y ángulo ($\theta$).

1. Cambio de Variables: $x^2+y^2$ se convierte en $r^2$.
2. El Diferencial de Área: $dA$ no es solo $drd\theta$. Debes multiplicar por el Jacobiano, que es $r$.$$dxdy\Rightarrow rdrd\theta$$
3. Nuevos Límites:
   • Radio ($r$): Como es un círculo de radio 2, $r$ va de $0$ a $2$.
   • Ángulo ($\theta$): Como es el círculo completo, $\theta$ da la vuelta entera, de $0$ a $2\pi$.

Sustituimos todo en la integral original:

Paso A: Integral interna (respecto a $r$)
Integramos $r^3$:

Paso B: Integral externa (respecto a $\theta$)
Ahora integramos la constante que nos quedó ($4$):

Resultado Final:

Coordenadas Cilíndricas (en 3D)

Extensión de las polares a 3D. Útil para cilindros, conos, paraboloides.

• Transformación: $x=r\cos \theta$, $y=r\sin \theta$, $z=z$

• Relación útil: $x^2+y^2=r^2$

• Elemento de volumen: $dV=rdzdrd\theta$

Coordenadas Esféricas (en 3D)

Útil para esferas y conos. (Convención ISO: $\rho$ = radio, $\varphi$ = ángulo polar (desde Z+), $\theta$ = ángulo azimutal (desde X+)).

• Transformación:

  • $x=\rho \sin \varphi \cos \theta$

  • $y=\rho \sin \varphi \sin \theta$

  • $z=\rho \cos \varphi$

• Relaciones útiles: $x^2+y^2+z^2={\rho }^2$, $x^2+y^2={\rho }^2{\sin }^2\varphi$

• Elemento de volumen (Jacobiano = ${\rho }^2\sin \varphi$): $dV={\rho }^2\sin \varphi d\rho d\varphi d\theta$

Ejercicios

Enlace.